Witam!

Istnieją dzisiaj rozwiązania o których Ci się nawet nie śniło. Naukowcy sądzą, że stanowią one ostateczne rozwiązanie problemu sztucznej inteligencji...

Wstęp

Gdy dowiedziałem się o istnieniu sieci neuronowych, a było to dawno, od razu mnie zainteresowały. Byłem wówczas pod wrażeniem "terminologii" użytej w jednym z filmów kanału "Discovery". Dostałem podręcznik do programu STATISTICA firmy StatSoft. Dwa miesiące później zacząłem gorączkowo przeszukiwać setki stron internetowych w poszukiwaniu przydatnych informacji. Minął pewien okres czasu zanim zdążyłem pojąć i zrozumieć podstawowe zasady tej "biologicznej technologii cyfrowej". Te strzępki informacji, które pojąłem - chce przekazać Wam.

Sieci neuronowe - co to jest?

Powszechnie określa się je mianem AI (od ang. Artifical Inteligence) lub SI (Sztuczna Inteligencja). Jak się okazuje - nie do końca słusznie gdyż Sieci Neuronowe są jedynie podzbiorem rozwiązań nazywanych AI. Do AI należą także algorytmy genetyczne, o których nie będę tutaj wspominał. Sztuczne Sieci Neuronowe (SSN) to temat rozległy. Nawet bardzo. W tym artykule opiszę zasadę ich działania, przedstawię pojęcia wag, warstw ukrytych i inne "egzotyczne" terminy dla nieobytego z tematem ucha. Zanim zaczniemy, chcę Cię prosić czytelniku, abyś po tym nudnym wstępie nie odchodził od lektury, ale czytał dalej, bo jak się zaraz przekonasz, ten artykuł nie jest kolejnym stekiem określeń z "wyższej półki", ale materiałem dla kogoś kto chce się dowiedzieć jak funkcjonują sieci i jak to się dzieje, że potrafią się uczyć.

Jak działa ludzki mózg ?

Dokładnie nikt jeszcze tego nie wie. Ale po lekturze tak wielu materiałów mam pewne przypuszczenia. W mózgu przeciętnego człowieka jest podobno około 100 miliardów neuronów. Są to bardzo niedokładne "przypuszczenia" i nie należy się nimi zbytnio sugerować. Biologiczny neuron jest komórką posiadającą wiele wejść (tzw. dendrytów) i tylko jedno wyjście (tzw. akson lub neuryt). Jego zadaniem jest po prostu przetworzenie danych z wejść i zwrócenie ich na wyjściu. Pojedynczy neuron nie ma zbyt dużej ilości pamięci, dlatego neurony łączą się ze sobą, tym samym powiększając swoje możliwości przetwarzania.


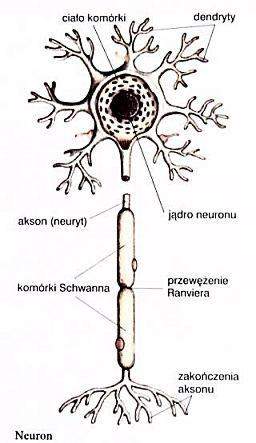
Kluczowym zagadnieniem w budowie biologicznego neuronu jest pojęcie synaps. Synapsy to rodzaj połączeń pomiędzy dwoma neuronami. Za ich pomocą sygnały mogą trafić od jednego neuronu do drugiego. To taki biologiczny rodzaj autostrady. Jednak synapsy nie spełniają tylko roli przekaźnika sygnałów. Są bardziej potrzebne niż się wydaje. Spełniają one jeszcze jedną kluczową rolę - wzmacniają lub osłabiają przekazywane sygnały. Może nie tyle wzmacniają czy osłabiają, ale są mniej lub bardziej drożne. To właśnie ta cecha synaps decyduje o prawidłowym działaniu sieci. Gdy neuron się uczy, synapsy, dzięki którym uzyskuje on prawidłowe wyniki na wyjściu "udrażniają się". Dzięki temu po paru "lekcjach" neuron jest w stanie zwracać poprawne wyniki.

Sztuczny model neuronu

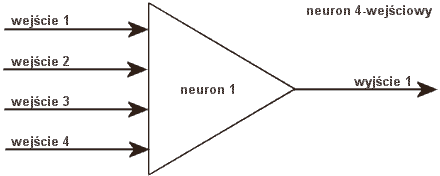
W sztucznym modelu wszystko jest bardzo podobne, z wyjątkiem tego, że "przepustowość synaps" zastąpiliśmy odpowiednimi mnożnikami. W sztucznym neuronie tym co robią synapsy zajmuje się operator iloczynu '*' ;) Nazwany jest on wagą i towarzyszy każdemu z wejść neuronu:


Gdy informacja trafia do wejścia jest ona przemnażana przez odpowiednią wagę. Przykładowo, mamy pewien sygnał - nazwijmy go Zdzich :) Gdy Zdzich wchodzi do wejścia numer 1 neuronu, wymnażany jest przez wagę numer 1. W efekcie mamy Waga1*Zdzich Zdzichów. Następnie gdy już wszystkie sygnały zostaną przemnożone przez te "odpowiedniki synaps dla ubogich", w neuronie jest wykonywana operacja sumowania wszystkich sygnałów, w ten sposób uzyskujemy tzw. "sumę ważoną wejść".

Funkcje aktywacji

Tak przetworzony sygnał zwykle przepuszczany jest przez tak zwaną funkcję aktywacji neuronu lub inaczej funkcję przejścia. "Zwykle", bo nie zawsze. Czasami suma ważona wejść (czyli sygnały z wejść przemnożone przez odpowiadające im wagi - następnie zsumowane) jest od razu zwracana na wyjściu jako ostateczna odpowiedź neuronu na wartości podane na wejściu. Tak proste rozwiązanie oczywiście nie może mieć miejsca w świecie, w którym wszystko jest skomplikowane, dlatego zwykle w neuronie dokładana jest jeszcze funkcja aktywacji. Ta funkcja aktywacji modyfikuje dodatkowo wartość ważonej sumy wag w najróżniejszy sposób.

Taka funkcja z ważonej sumy wag może zrobić na przykład wartość dwustanową (0 lub 1). Wtedy taką funkcję nazywamy progową, ponieważ dla wartości np. mniejszych lub równych 0 przyjmuje ona wartość 0, a dla większych od 0 przyjmuje wartość 1.

Najczęściej jednak funkcje tak bardzo ograniczające możliwe odpowiedzi neuronu (do dwóch stanów 0 lub 1) nie mają zastosowania w praktyce. Neuron zwraca bowiem najczęściej jakąś tam wartość z rozwinięciem dziesiętnym do kilku miejsc po przecinku. Nielogiczne byłoby tak "dokładny" sygnał obcinać do dwóch wartości (0 i 1). Dlatego stosuje się funkcje nieliniowe, które co prawda zawężają wartość wyjściową do przedziału np. (od 0 do 1), ale pozwalają przyjmować wartości pośrednie jak np. 0,2324 czy 0.8764. Funkcje progowe takich właściwości nie mają - one sztywno ustalają czy neuron ma zwrócić 1 czy 0 (bez wartości pośrednich).

Istnieją najróżniejsze typy funkcji aktywacji. Czasami ich nazwy mogą przyprawić niektórych o ból głowy, ale zapewniam, że wszystkie one spełniają to samo zadanie:

Legenda:
y - wartość zwracana przez funkcję, a jednocześnie wartość wyjściowa neuronu
suma_w - suma ważona wejść neuronu
beta - współczynnik stromości krzywej
alfa - współczynnik szybkości uczenia


Niektóre z dostępnych dzisiaj funkcji:

1. Funkcja liniowa
   Brak funkcji ;) Suma ważona wejść jest zwracana bezpośrednio na wyjściu.
   y = suma_w
2. 'Obcięta' funkcja liniowa
   Sygnał wyjściowy należy do przedziału (-1 do 1). Jeżeli suma_w < -1 to y=-1, jeżeli suma_w > 1 to y=1, w pozostałych przypadkach y=suma_w, np. jeżeli suma_w = 0.7 to y=0.7.
   y = -1 jeżeli suma_w < -1 y = 1 jeżeli suma_w > 1 y = suma_w jeżeli (suma_w <= 1) lub (suma_w >= -1)
3. Funkcja progowa unipolarna
   Przyjmuje ona wartość 1 (czyli y=1) gdy suma_w >= 0, natomiast y=0 gdy suma_w<0.
   y = 1 jeżeli suma_w >= 0 y = 0 jeżeli suma_w < 0
4. Funkcja progowa bipolarna
   y = -1 jeżeli z < 0 y = 1 jeżeli z >= 0
5. Funkcja sigmoidalna unipolarna
   Wyrażona jest wzorem:
   y=1/(1+exp(-beta*suma_w))
   Jest najczęściej stosowaną funkcją w dziedzinie sieci neuronowych, a to dlatego, że jej wykres jest bardzo płynny, w przeciwieństwie do funkcji progowych, gdzie następuje gwałtowny skok. Funkcja ta ma większe możliwości w stosunku do progowych i pozwala neuronowi określić na ile jest "pewien" swojego wyniku. Przyjmuje wartości od zera do 1.
6. Funkcja sigmoidalna bipolarna
   Wyrażona jest wzorem:
   y=2/(1+exp(-beta*suma_w))-1
   Jest to modyfikacja funkcji sigmoidalnej unipolarnej. Rozszerzono w niej zakres możliwych do przyjęcia wartości (funkcja może przyjąć wartość z zakresu od -1 do 1) - stąd nazwa bi (dwa) [uni - jeden].
7. Funkcja "tangens hiperboliczny"
   Wyrażona jest wzorem:
   y=(1-exp(-alfa*suma_w))/(1+exp(-alfa*suma_w))
   lub
   y=tanh(beta*suma_w)
   Funkcja wyglądem przypomina funkcję sigmoidalną bipolarną. Przyjmuje wartości od -1 do 1.
8. Funkcja sinusoidalna
   Wyrażona jest wzorem:
   y=sin(beta*suma_w)
9. Funkcja cosinusoidalna
   Wyrażona jest wzorem:
   y=cos(beta*suma_w)

Funkcji jest dość dużo jak widzicie. Jak powiedziałem, nie musicie ich stosować w prostych sieciach neuronowych. Prostych to znaczy, gdy sieć nie posiada warstw ukrytych. Powyższe funkcje to raczej bardziej ciekawostka niż dane do budowy dużej sieci. Do budowy takiej nieco "większej" sieci wykorzystuje się właśnie te funkcje wraz z ich pochodnymi. Pochodne wyznaczamy dla każdej z funkcji:

• pochodna sigmoidalnej
  f '(x) = beta*[1-f(x)]*f(x)
• pochodna tangensu hiperbolicznego
  f '(x) = beta[1-f 2(x)]
• pochodna sinusoidy
  f '(x) = beta*pierwiastek[1-f2(x)]
• pochodna cosinusoidy
  f '(x) = -beta*pierwiastek[1-f2(x)]

Podałem to, ponieważ chciałbym aby te wzory stanowiły oparcie dla was w przyszłości. Jeśli nie rozumiesz to na razie nic się nie dzieję. Jak mówiłem na początku nie będzie Ci to potrzebne, ponieważ możesz konstruować sieci neuronowe z całkowitym pominięciem funkcji aktywacji. Model neuronu z funkcją aktywacji wygląda następująco:


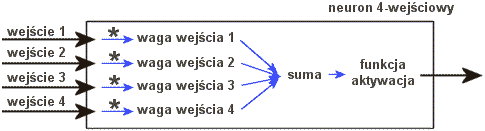
Bez funkcji aktywacji tak:

Programy oparte na sieciach neuronowych

Programy działające w oparciu o sieci neuronowe mogą działać cuda. Takie programy najczęściej z powodzeniem stosuje się np. do rozpoznawania pisma tzw. OCR (nie wszystkie OCR-y działają jednak w oparciu o sieci neuronowe). Za pomocą SSN możemy także kontrolować pracę maszyn, np. silnika samochodu - ograniczając tym samym np. zużycie paliwa. Dobrze nauczona sieć jest doskonałym narzędziem statystycznym. To prawdziwy "oręż" oddany w ręce ludzi zajmujących się statystyką stosowaną.

Jak działa program symulujący działanie sieci neuronowej? Ilustrują to poniższe kroki:

1. Pobranie wartości wejściowych (wartości podanych przez użytkownika) Wartości wejściowych i wartości oczekiwanej jaka pojawić się ma na wyjściu
2. [krok wykonywany przy pierwszym uruchomieniu] : Losowa generacja wag, czyli przypisywanie wagom małych losowych liczb (najczęściej różnych od 0, np. 0.34532) Ten krok ma szczególne znaczenie, ponieważ jeśli go nie wykonamy wartości wejściowe neuronu będą mnożone przez 0, w wyniku czego zawsze otrzymamy 0.
3. Przepuść pojedynczy sygnał przez sieć W wyniku tej operacji podane na wejściu neuronów wejściowych wartości wejściowe podane przez użytkownika są w każdym neuronie wymnażane przez odpowiadające im wagi (suma ważona wejść) i zwracane na wyjściu (mogą przejść także przez funkcję aktywacji, która dodatkowo "uszlachetni" te wartości i przyporządkuje je do podanego zakresu). Tak obliczone wartości wyjściowe są równocześnie wartościami wejściowymi neuronów z następnej warstwy, itd...
4. Oblicz błąd na wyjściu sieci
   Oblicz błąd wyjściowy sieci odejmując od wartości oczekiwanej przez użytkownika wartość zwróconą przez sieć w trakcie "pojedynczego przetworzenia"
5. Oblicz błędy na każdym z neuronów sieci
   W przypadku gdy korzystamy z funkcji aktywacji tutaj korzystamy z wartości pochodnych funkcji, w przypadku gdy takowej nie używamy korzystamy z innych wzorów. Ja skorzystałem z takiego (nie wiem do tej pory czy jest poprawny ;):BladNeuronu[numerWarstwy][numerNeuronu] = BladNeuronu[numerWarstwy][numerNeuronu] + Output[numerWarstwy][numerNeuronu] * BladNeuronu[numerWarstwy+1][numerWagi] * Waga[numerWarstwy+1][numerWagi][numerNeuronu]umerWarstwy+1 oznacza, że chodzi o następną warstwę.
6. Uwzględniając błędy obliczona na każdym neuronie sieci dopasuj odpowiednio wagi (powiększ lub pomniejsz)
   Tu też pewny udział ma w przypadku korzystania z f. aktywacji, pochodna tej funkcji. Szukajcie w innych bardziej fachowych materiałach, jakich wzorów możecie użyć w tym przypadku. Tam Was właśnie odsyłam, gdy będziecie chcieli zbudować sieć np. wielowarstwową.
7. Powyższe kroki powtarzaj do momentu kiedy poziom błędu sieci będzie mniejszy od minimalnego dopuszczonego poziomu błędu, np. 0.01
   Aby zakończyć cały proces musi być spełniony warunek: Blad < dopuszczalnyBlad

Programy do eksperymentów

Istnieje kilka aplikacji, które umożliwiają budowę i pracę z sieciami neuronowymi. Program który bardzo utkwił mi w pamięci jest EasyNN ( www.easynn.com/) - pozwala na budowanie złożonych sieci neuronowych, ich uczenie i korzystanie z nich, jednak aby go obsłużyć należy już co nieco wiedzieć o sieciach neuronowych (wiadomości z tego artykułu powinny Wam wystarczyć).
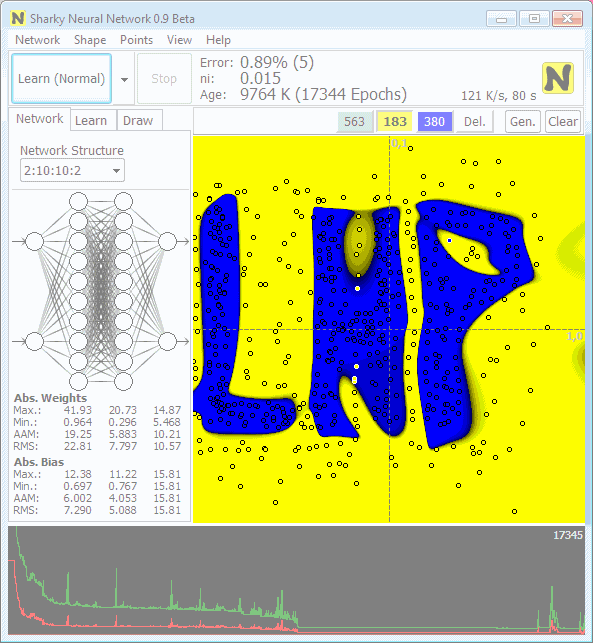
Drugim z kolei programem jest polski Sharky Neural Network ( www.sharktime.com). Jest on dużo łatwiejszy w obsłudze niż EasyNN (choć pod maską kryją się równie skomplikowane mechanizmy), jednak ma nieco mniejsze możliwości - w zasadzie służy on do czego innego - umożliwia klasyfikację zbiorów za pomocą sieci neuronowych (może posłużyć do ilustracji rozwiązania typowego problemu oddzielenia od siebie punktów o różnych cechach). Należy zaznaczyć, że przy jego pomocy można rozwiązywać wiele problemów - wymaga to jednak od nas odpowiedniej interpretacji punktów. Może przykładowo posłużyć do rozwiązania typowego problemu XOR - problemu z którym nie radzi sobie pojedynczy neuron ([dla ciekawych]: pojedynczy neuron nie radzi sobie z problemem XOR z tego względu, że w problemie XOR musimy rozdzielić obszary za pomocą dwóch prostych, a stosując pojedynczy neuron jest możliwość oddzielenia za jego pomocą co najwyżej dwóch obszarów poprzez jedną prostą - prosta dzieli nam dwuwymiarową przestrzeń naco najmniejdwa obszary - czyli innymi słowy pojedynczy neuron umożliwia nam klasyfikowanie rzeczy jedynie do dwóch worków), aby go rozwiązać należy zastosować co najmniej dwa neurony (tzn... w zasadzie najwłaściwiej jest zastosować coś zbliżonego do dwóch neuronów - to jest tak jak z ludźmi - im człowiek ma większą wiedzę i możliwości umysłowe tym mniej go interesują rzeczy proste, nie zastanawia się nad nimi - woli je od razu zapamiętać. Podobnie nadmiarowe sieci (z ilością neuronów znacznie większą niż jest potrzebna) mają tendencję do "zapamiętywania" problemów, a nie ich rozwiązywania. Jak te twory nam nas przypominają, prawda? :-)

Zakończenie

Poznaliśmy pojęcia Neuronów, Wag, Warstw, funkcji aktywacji neuronu, sumy ważonej wejść i innych. Mam nadzieję, że artykuł wzbudził Wasze zainteresowanie. Przekazałem Wam część wiedzy na temat tego zagadnienia, a problemy nad którymi wiele myślałem zaprezentowałem w bardziej przystępny sposób, a to wszystko po to aby kolejne pokolenia mogły coraz prościej myśleć o "Sztucznych Sieciach Neuronowych". Dziękuję!