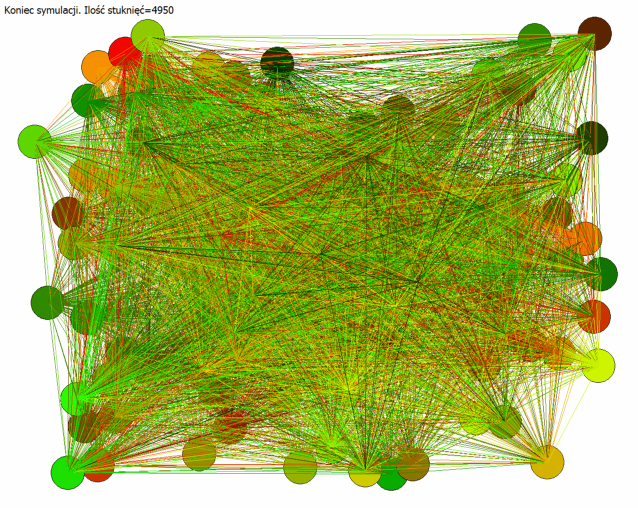
Problem biesiadników - czyli jak stuknąć się ze wszystkimi na weselu
Sat, 28 March 2015
Będąc wczoraj na spotkaniu ze znajomymi zaciekawił mnie problem obliczenia ilości stuknięć kieliszków, tak, aby każdy stuknął się z każdym dokładnie raz.
Jak to z programistami bywa, takie problemy - choć zupełnie absurdalne - nie dają człowiekowi spokoju dopóki nie zostaną ostatecznie rozwiązane. Ten akurat - na moje szczęście - nie był zbyt skomplikowany, a gdy wytrzeźwiałem z wody mineralnej - okazał się prosty. Dlatego w tym artykule szybko przedstawię jego rozwiązanie.
Rozwiązanie
Rozwiązując dowolny problem matematyczny, bardzo przydatnym jest spojrzeć na przypadki brzegowe. Tak zazwyczaj bywa, że niosą one kluczowe informacje. Rozpatrzmy więc jak problem będzie się prezentował dla różnych ilości biesiadników ( n ). Jeśli nie mamy żadnego biesiadnika, liczba potrzebnych stuknięć powinna wynieść 0. Jeśli mamy jednego biesiadnika - tak samo. Jeśli dwóch - nie mają oni innej możliwości, jak "stuknąć się" pomiędzy sobą.

Przy trzech biesiadnikach, zaczyna pojawiać się prawdziwe oblicze: bowiem pierwsza osoba musi stuknąć się z drugą i trzecią, jednak trzecia powinna również stuknąć się z drugą. Dla n=3 potrzeba więc 3 stuknięć.

A co z czterema osobami? Najpierw pierwsza osoba stuka się z każdą z pozostałych osób (a więc dwójką, trójką i czwórką), a następnie dwójka stuka się ze wszystkimi osobami prócz osób, które "inicjowały" stuknięcie uprzednio (tak więc dwójka stuka się teraz z trójką i czwórką, ale nie z jedynką). Trójka podobnie jak dwójka - stuka się ze wszystkimi prócz osób, które uprzednio "inicjowały" stuknięcia (tak więc stuka się jedynie z czwórką). Czwórka nie stuka się już z nikim, bo ze wszystkimi się już stuknęła. W wyniku tej sekwencji, liczba potrzebnych stuknięć dla n=4 wynosi 6.

Spróbujmy zatem na podstawie tego opisu ustalić wzór rekurencyjny, a następnie wzór zwarty dla potrzebnej ilości stuknięć. Widzimy, że sumę stuknięć dla przypadku n=4 możemy zapisać jako dodawanie:
S = (n-1)+(n-2)+(n-3)Co daje nam następującą sumę:

Końcowym krokiem rozpracowywania problemu jest opisanie go za pomocą wzoru zwartego, czyli takiego, który nie zawiera w sobie rekurencji, czyli obliczeń dla n innych niż aktualne. Aby tego dokonać, musimy zauważyć, że suma podciągu (1..n-1) wzrasta stopniowo, średnio o wartość (n-1)/2. Stosując więc wzór na sumę ciągu arytmetycznego otrzymujemy wzór zwarty:
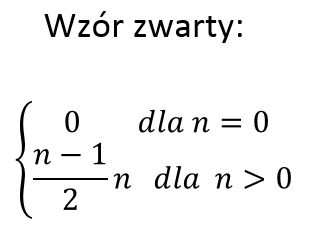
Złożoność
Złożoność obliczeniowa wzoru rekurencyjnego jest jak O(n2). Złożoność wzoru zwartego to oczywiście O(1).
Jak zrobić to najszybciej w świecie fizycznym?
To proste. Należy ustawić ludzi w rzędzie. Ostatnia osoba z rzędu się wyłamuje i idzie wzdłuż rzędu (od jego końca do początku) stukając się ze wszystkimi kieliszkami. Następnie wyłamuje się przedostatnia osoba (aktualnie ostatnia) i robi to samo (osoby nie wracają już do rzędu). I tak dalej. Kiedy kolej na wyłamania się z szeregu dojdzie do pierwszej osoby wszyscy będą mogli być pewni, że stuknęli się kieliszkami dokładnie raz :)
Program symulujący
Napisałem program, który symuluje nam stuknięcia kieliszków dla dowolnej liczby osób. Ma możliwość generowania i zapisywania plików graficznych do pliku, co umożliwiło stworzenie animacji dla niniejszego artykułu. Aplikację można pobrać stąd.
Do artykułu dołączam również arkusz kalkulacyjny dotyczący opisywanego problemu.
Klip wideo
Zakończenie
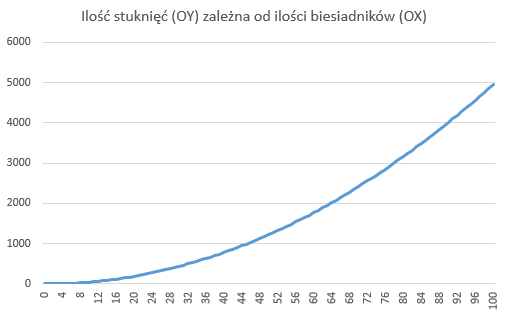
A co z przypadkiem dla 100 osób? Potrzeba na nich 4950 stuknięć, aby każdy był usatysfakcjonowany :)